| ||
| | ||
| コンテンツ | ||
| はじめに | ||
| トーンリプロダクション | ||
| O/G変換 | ||
| icc profile のグラビア的利用 | ||
| プロ用製版スキャナー | ||
| 仕事に役立つ 視覚の法則 | ||
| 版の精度とは何か? | ||
| グラビア版の値段 | ||
| グラビア製版エキスパート試験 | ||
| 今後まとめようと思う項目 | ||
| 更新履歴 サイト作成 | ||
| DTPエキスパート認証試験 独学受験必勝法 | ||
| my personal affair | ||
DTPに役に立つリンク集↓ | ||

Photo by 尾島 孝一
視覚の法則>濃度の法則
濃度の法則
スキャナーのオペレーター時代に
「濃度の単位は何?」とか「濃度はいくつまであるの?」とよく聞かれました。
いつも濃度計は使っていましたが、答えられませんでした。
そんなこと知らなくても仕事はできるし、調べればわかることだと思っていました。
が、今になってインターネットで検索しても、理解できる答えがどこにもないんです。私は数学は大嫌いな科目だったので、自分でこんなこと書くのはすごく気が引けるし、ーーーでも、ま〜「どこにも答えが無いんだからしょうがない、自分で答えを書いちゃえ!」ということで
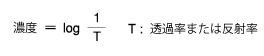
この式は、この関係の資料を調べればすぐでてきます。わからないのはこの意味です。
「あなたもたぶんそうでしょう」(^_^;
ということにして以下進めます。
なんか「文系の人の数学講座」みたいですが、要はlogの理解度にあるんです。
よくわからないんですよ logがね〜私には〜
でも強引に自説を展開しちゃいましょう!
「DTPエキスパート試験」の出題項目で「2進法」の項目があったと思いますが、logも、それに非常に似ています。
たとえば、日本語じゃなくて英語で言うみたいな感覚、意味は同じなんですが、なんで英語で言うのか? というと、「かっこいいから」ってな理由があげられると思いますが、
logの場合は「そうすると人が理解し安くなるから」となります。
人は日常的生活で123456789…と数える時に1と2の間隔と8と9の間の間隔は同じ1であると考えますよね。(これを間隔尺度と言います)
お金で言うなら、400円と500円の差は100円、9900円と1万円の差も100円、と同じ差です。実際問題、500円の時と1万円の時で100円の価値に差があったのでは買い物が大変です.(*1)
しかし、人間の知覚の感覚はそうなっていないんです。
そこにlogを使う効能があるんです。
人は物を見る時、薄い色の時の100円の差と濃い時の100円の差が違うんです。薄い時も濃い時も、同じ100という数字なんですが、濃い時の100円は1万円位のお金をださないと薄い時の100円分の濃度差と同じに見えないように人の目はなっているのです。
「いやー、でも井上さん、その話はにわかには信じ難い、だって、私の目はそうゆうふうには見えてませんよ!」
と言う人は多いでしょう。
私も同感です。でも物理学的には、どうもそういうことらしいんです。
文系の人は自分の感覚を基準にして計るが、理系の人は物理法則の方を優先して基準にするのだ、と考えれば少しは納得がいくでしょう。
透過率だけで表わすと全透過の100%からほとんど透過しない0.01%まで、なんと10000倍差があります(これは濃度0.0〜4.0までの例。3.0までなら〜0.1%までで1000倍の差になります)
数が増えすぎるからlogを使うと言う説明をしている資料もありますが、それは見当はずれです。千倍でも1万倍でも等歩度(直線的変化)になってれば,logという概念は必要ありません。
ですので最初の問題の答えは
「濃度とは?」
透過率(反射率)というものさしを目のものさしにあわせて、人に理解できるように変換した数字、それが濃度なんです。
ちなみに、理系的答えは「濃度とは透過率(反射率)の逆数の対数である」です なんのこっちゃいな? ですよね
「濃度の単位は何?」
濃度の単位は無いんです、どうしても付けたければ、数字の後にODと付けてるサイトを発見しました。(光学濃度、Optical Densityです)
個人的には Visual Ruler でVRなんて単位をつけたらどうかと思います。
「ベタ濃度は?」「1.65VRです」 どうです?やはり変か?
さらに余談ですが、製版で扱う濃度は正確には(光学濃度、写真濃度)と言います。
「濃度はいくつまであるの?」
透過率100%は濃度0、透過率0%は計算上は濃度∞です。(そもそも透過率0%という概念はないらしい)
以下、透過率0%は計算上は濃度∞ を、説明します。
| 濃度計などの測定機では、以下のような計算が計器内部で行われて網点%を表示しています。(数字はたとえばの数字) | |
|---|---|
| 1、白地を計る | 0.05 |
| 2、ベタを計る(通常この作業はない) | 1.65 |
| 3、網点%を知りたい部分の濃度 | 0.79 |
| 濃度計内部で以下の計算が自動的に行われます | |
| =(1-10^-(0.79-0.05))/(1-10^-(1.65-0.05))*100 | |
Excel や FileMaker などに、この式をコピー&ペーストしてもらえれば83.91073375=84%となります。 |
|
| 答え:(この条件だと濃度0.79 は) | 84% |
続いて、なぜベタを計る作業は省略できるのか?の説明をします。
0.05 |
0.3 |
0.5 |
1.0 |
1.5 |
2.0 |
3.0 |
5.0 |
10.0 |
|
| ベタ濃度 1.5 | 0 |
45.4 |
66.9 |
92.0 |
100.0 |
||||
| ベタ濃度 2.0 | 0 |
44.3 |
65.3 |
89.8 |
97.5 |
100.0 |
|||
| ベタ濃度 3.0 | 0 |
43.8 |
64.6 |
88.9 |
96.6 |
99.0 |
100.0 |
||
| ベタ濃度 5.0 | 0 |
43.8 |
64.5 |
88.8 |
96.5 |
98.9 |
99.9 |
100.0 |
|
| ベタ濃度10.0 | 0 |
43.8 |
64.5 |
88.8 |
96.5 |
98.9 |
99.9 |
100.0 |
100.0 |
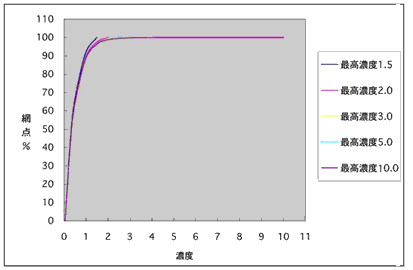
ベタ濃度が大きく変化しても、濃度1.5ぐらいまではグラフが重なっているのがわかると思います。そうなんです、無限大というとスゴク濃いところまであって調子全体が濃くなると思ってしまいますが、そうではなく、最高濃度が2でも10でも中間の1.0や1.5の網%はほとんど変化しません。印刷物の調子というものはスゴク暗いところがあるからといって それにひきづられて明るいところや中間調が濃くなったりしないんです。
ですから、最高濃度がどんなに黒くても調子に影響しないということで∞というアバウトな数字でもOKなんです。キャッチライトという言葉がありますが、これはキャッチシャドウと言えるでしょう。キャッチシャドウも調子管理範囲に含めてはいけない管轄外の調子です。
以上「濃度はいくつまであるの?」の説明:2008.3.25追加
ここまで説明して恐縮なんですが、実は
濃度はマンセル値みたいに見た目に等間隔になっている数字ではありません!「おいおい、話がおかしいじゃないか!井上さん」と言われそうですが
視覚的には完全には等歩度にはできていないみたいです。
たまたま、このlogの式にあてはめると数字が知覚的に等歩度に近くなることを発見した人がいて、それ以降、濃度(log)という数字を使うようになったのではないでしょうか?(これは私の強引な仮説です、そう考えた方が文系的頭脳には非常に理解しやすいんですが…)
下の図は網点の法則のページで使った表ですが、これで等間隔でない証拠をお目にかけましょう。
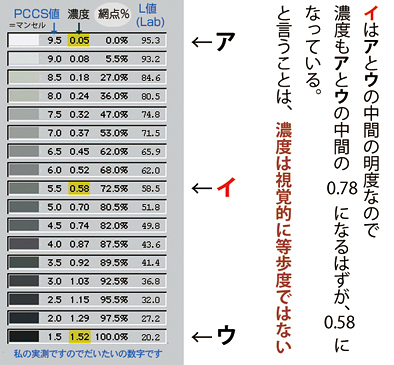
でも、そんな極端にかわらないので,実際の仕事では濃度は視覚的に等間隔と考えて問題ないと思います。
もう濃度は時代遅れの単位と言う人が居ますが、印刷という職業が続く限りなくならないでしょう。
一応これで説明終了です。
おわりなんですが、ここまで読んで、
「じゃー、透過率とか反射率ってなんなんだ?」と思った方は、ただならぬ探究心の持ち主です。
「ひょっとしたら、それは網点面積率と同レベルのものじゃないのか?」
そう思った方はさらに鋭い。
この続きは次回更新までお待ちください。理系語を文系語変換してきます。
(*1)の補足説明:
実際問題、500円の時と1万円の時で100円の価値に差があったのでは買い物が大変です。と言う例ですが、心理的には差がありますよね。
たとえば缶コーヒー、駅の構内だと130円と高いのでコンビ二で120円で買って飲むことがあると思います、10円得しましたね。この差の感覚は5000万円の家を買う時にはどうでしょう?300万円引きの4700万円になったぐらいの感じと同じじゃないでしょうか?(でも、この場合は比例の問題で今回の対数の話とはちょっと違います)
2008.1.4


